Coordinate systems
Computers and Mathematics have a different notation when it comes to co-ordinate systems.
In Mathematics, y value of a point increases if the point moves up.
But, in pixel system (2D computer graphics), y increases as we go down.
You can drag the sliders in the below displayed flash controls
and see how the (x, y) values change in the normal (mathematics) co-ordinate system and computer's pixels window co-ordinate system.
NEED FOR CONVERSION FROM ONE SYSTEM TO THE OTHER:
For a single unique mathematical graph (in normal system), there could be multiple converted graphs depending on the viewport dimensions.
For example, consider a rectangle ABCD in the normal system.
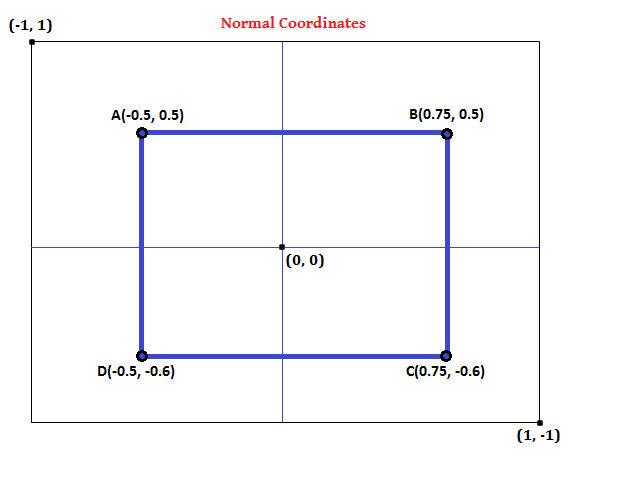
If the same rectangle has to be drawn in a viewport with the dimensions (640, 480), the point A becomes(160, 120).
If the same rectangle has to be drawn in a viewport with the dimensions (800, 600), the point A becomes(200, 150). (HOW???)
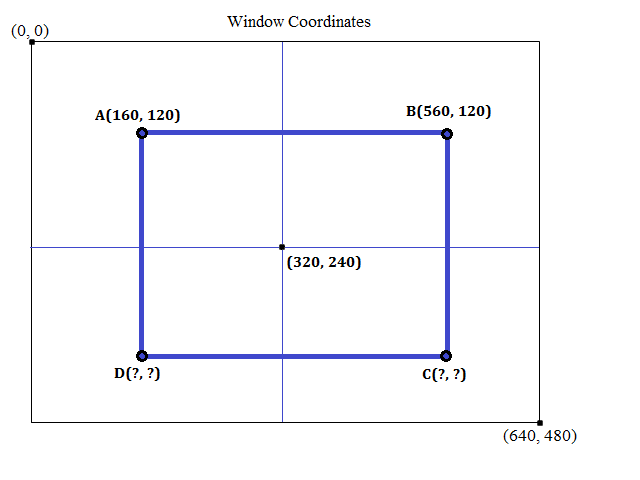
CONVERSION:
If we have to convert a value from the range (-1 to 1) into a value in the range (0 to 640), we use the following formula(WHY???)...
x' = (x*0.5 + 0.5)*640
If we have to convert a value from the range (1 to -1) into a value in the range (0 to 480), we use the following formula(WHY???)...
y' = (0.5 - y*0.5)*480
If we have to convert a value from the range (0 to 640) into a value in the range (-1 to 1), we use the following formula(WHY???)...
x' = (x/320.0) - 1
If we have to convert a value from the range (0 to 480) into a value in the range (1 to -1), we use the following formula(WHY???)...
y' = 1 - (y/240.0)
EXERCISES:
(1) Consider the rectangle ABCD in the normal system. Use the above formulae and verify
if the points A and B of the window system's rectangle ABCD are properly converted or not.
(2) Calculate the points C and D in the window system.


