Perspective projection matrix
A VERY OLD STUPID JOKE:
| Idiot-A: | Hey!!! Look!!! An aeroplane!!!
|
| Idiot-B: | I wonder who has the patience to paint such a huge plane!!!
|
| Idiot-C: | When the aeroplane goes far into the sky, it becomes so small. And then, any painter can easily paint that tiny aeroplane. |
Consider a group of boxes arranged on the floor

The nearer boxes appear bigger.
And the farther boxes appear smaller.
Perspective projection
In computer graphics, we often face the situation to transform a
view-frustum into a cuboid shape. The motive behind this transformation
is to
achieve the realistic effect of diminishing the size of the graphics
objects as they move away from the camera.
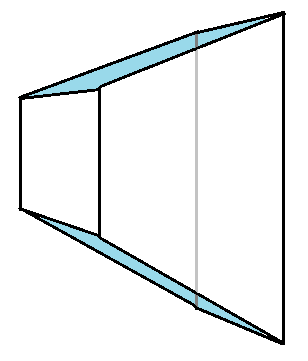
The above volume should be transformed into...
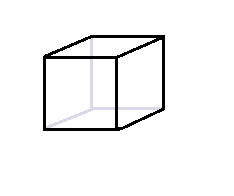
And, as you have guessed it, this transformation is done through the matrix multiplication.
Before getting deeper into the problem, let's observe the transformation a little closer.
Inputs:
1. width of the viewport
2. height of the viewport
3. near plane distance from the camera
4. far plane distance from the camera
5. θ - the field of view
Output:
A 4x4 matrix
We need a 4x4 matrix, that can transform
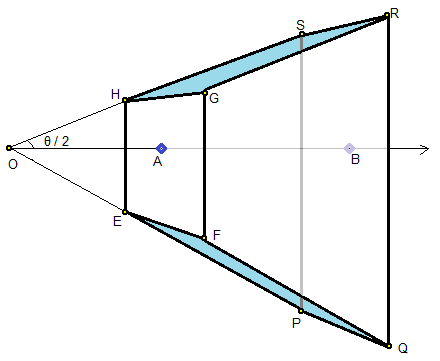
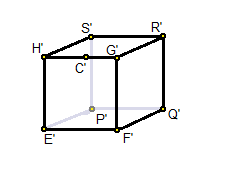
the frustum EFGHPQRS into...
the cuboid E'F'G'H'P'Q'R'S'
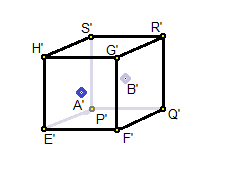
Formal representation:
Lets consider the points A and B on the camera's direction
A is a point on the near plane with the coordinates A(0, 0, near).
B is a point on the far plane with the coordinates B(0, 0, far).
Recall from the previous page that, when we add a 4th component, we get the following 4D coordinates...
A(0, 0, near, 1) and B(0, 0, far, 1)
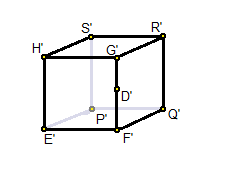
Now, consider the cuboid E'F'G'H'P'Q'R'S' in which...
On X-axis (parallel to E'F'), left = -1 and right = 1
On Y-axis (parallel to E'H'), top = 1 and bottom = -1
On Z-axis (parallel to E'P'), front = 0 and back = 1
Then, we have A'(0, 0, 0) and B'(0, 0, 1)
If these are to be projected at a unit distance from the camera(or origin), we get the following 4D coordinates...
(0, 0, 0, 1) and (0, 0, 1, 1)
Recall from the previous page that a point(x, y, z, w) is same as (x/w, y/w, z/w, 1)
So, we can have...
A'(0, 0, 0, near) and B'(0, 0, far, far)
Solving for the matrix:
The 4x4 matrix should transform the vectors A into A' and B into B'
Lets Assume the matrix is given by...
| M = |
m11 | m12 | m13 | m14 |
| m21 | m22 | m23 | m24 |
| m31 | m32 | m33 | m34 |
| m41 | m42 | m43 | m44 |
M x A = A'
| m11 | m12 | m13 | m14 | X | 0 | = | 0 |
| m21 | m22 | m23 | m24 | 0 | 0 |
| m31 | m32 | m33 | m34 | near | 0 |
| m41 | m42 | m43 | m44 | 1 | near |
That gives us...
| near.m13+m14 | = | 0 |
| near.m23+m24 | 0 |
| near.m33+m34 | 0 |
| near.m43+m44 | near |
Similarly, if we take M x B = B' then we get...
| far.m13+m14 | = | 0 |
| far.m23+m24 | 0 |
| far.m33+m34 | far |
| far.m43+m44 | far |
Solving the above simultaneous equations, we get...
m13 = 0
m14 = 0
m23 = 0
m24 = 0
m44 = 0
m43 = 1
m33 = far / (far - near)
m34 = near.far / (near - far)
Now, our matrix looks like...
| M = |
m11 | m12 | 0 | 0 |
| m21 | m22 | 0 | 0 |
| m31 | m32 | far / (far - near) | near.far / (near - far) |
| m41 | m42 | 1 | 0 |
Cool. We have already found half the values of the matrix. For the remaining half, here we go...
(Go and have a cup of coffee if you need a break)
Now, consider the point C which is the mid point of GH
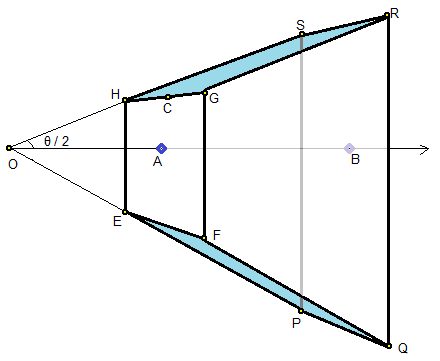
When viewed from the side angle, it looks like this...
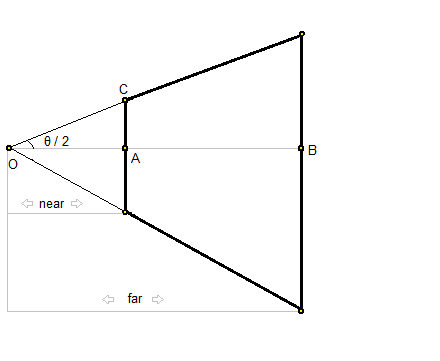
With little trigonometric workout, we can deduct...
C(0, near.tan(θ/2), near, 1)
And it's counterpart on the cuboid would be a 4D version of (0, 1, 0)
C'(0, near, 0, near)
M x C = C'
| m11 | m12 | m13 | m14 | X | 0 | = | 0 |
| m21 | m22 | m23 | m24 | near.tan(θ/2) | near |
| m31 | m32 | m33 | m34 | near | 0 |
| m41 | m42 | m43 | m44 | 1 | near |
Substituting the already found values will give us...
| m11 | m12 | 0 | 0 | X | 0 | = | 0 |
| m21 | m22 | 0 | 0 | near.tan(θ/2) | near |
| m31 | m32 | far / (far - near) | near.far / (near - far) | near | 0 |
| m41 | m42 | 1 | 0 | 1 | near |
That give us...
| m12.near.tan(θ/2) | = | 0 |
| m22.near.tan(θ/2) | near |
| m32.near.tan(θ/2) | 0 |
| m42.near.tan(θ/2) + near | near |
And a little algebraic workout will give us...
m12 = 0
m22 = cot(θ/2)
m32 = 0
m42 = 0
Now, our matrix looks like...
| M = |
m11 | 0 | 0 | 0 |
| m21 | cot(θ/2) | 0 | 0 |
| m31 | 0 | far / (far - near) | near.far / (near - far) |
| m41 | 0 | 1 | 0 |
Cool. We are almost there. We just need one more column in our matrix.
Now, consider the point D, which is the mid-point of GF
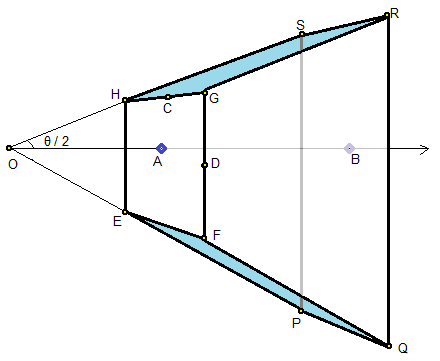
Recall that A is the center of the Rectangle EFGH
And C is the mid-point of GH
From the image, we can say that AD / AC = width / height
If we represent the width / height value as 'aspect' ratio, we get...
D(aspect.near.tan(θ/2), 0, near, 1)
And its counterpart on the cuboid would be a 4D version of (1, 0, 0)
D'(near, 0, 0, near)
If we consider M x D = D' then we get...
| m11 | 0 | 0 | 0 | X | aspect.near.tan(θ/2) | = | near |
| m21 | cot(θ/2) | 0 | 0 | 0 | 0 |
| m31 | 0 | far / (far - near) | near.far / (near - far) | near | 0 |
| m41 | 0 | 1 | 0 | 1 | near |
That give us...
| m11.aspect.near.tan(θ/2) | = | near |
| m21.aspect.near.tan(θ/2) | 0 |
| m31.aspect.near.tan(θ/2) | 0 |
| m41.aspect.near.tan(θ/2) + near | near |
And a little algebraic workout will give us...
m11 = cot(θ/2) / aspect
m21 = 0
m31 = 0
m41 = 0
Finally, our matrix looks like...
| M = |
cot(θ/2) / aspect | 0 | 0 | 0 |
| 0 | cot(θ/2) | 0 | 0 |
| 0 | 0 | far / (far - near) | near.far / (near - far) |
| 0 | 0 | 1 | 0 |
EXERCISE:
1) This derivation was based on the assumption that the near plane corresponds to the Z-axis value of front = 0 on the cuboid.
Find the projection matrix if the near plane corresponds to Z-axis value of front = -1 on the cuboid.
2) This derivation was also based on the left handed coordinate system,
where front has lesser value than the back.
Find the projection matrix for the right handed coordinate system, where
the Z-axis values are front = 1 and back = -1 on the cuboid.










