How much to save? How much to spend?
FOREWORD :

A decade back (in 2004), some hotels used to serve full-meals (Commonly known as "unlimited Thaali" in other parts of India) for 10 rupees. A 19 year old teenager with 75+ kg body weight and 170 cm body height with his hyper-hunger driven by his still growing body could eat as much as he could - within that 10 rupees worth food. (Of course, it was tasty, healthy and clean). Fast forward 10 years to the present 2014... and a cafe charged him 100 rupees for a cup of coffee.

A decade back, that same 19 year old boy, after taking up a lot of part-time odd-jobs like a sales-boy, a delivery-boy, a home-tutor, a typist etc. could manage to save 3000 rupees in an year. Fast forward 10 years, the same guy, now 29 years old, if he likes a pair of shoes and learns that the cost of those shoes is 3000 rupees (the exact amount equal to the annual savings he could manage a decade back), what would be his thoughts before deciding to buy those shoes or not?

The question here is... not if that guy can afford the money (of course... he can afford :P )

But the questions in his mind are...

It is just a YES/NO question. But, there is a lot of internal conflict involved in it.

Roughly all those questions get funnelled down to..

Well, I admit. A lot of us get through the exact same doubts. Especially when our facebook friend shares an image, saying that for every 1000 shares, a garbage scavenging poor hungry kid somewhere can get a kg rice, and the same friend shares the photos he took from a foreign beach where he has spent 50% of his life-time-savings for a 3 night stay in some costly hotel.

That's ok. The good old (millennia old) Indian rules to our rescue. They don't add any drama or unnecessary complications. They simply suggest that an earning person should be willing to do equal justice to all of the above.

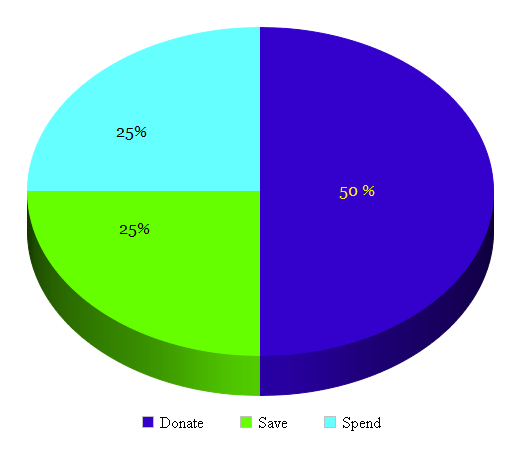
Translation? Well, you see... Spend half your income for the society. Use the remaining half for yourself. Out of this remaining part, use 50% for saving. And spend the rest.

For example, if you are earning 100,000 rupees per month, according the good old Indian Dharma rules, you should be giving away 50,000 to help the needy in the society. And out of the remaining 50,000 rupees, if you save 25,000 rupees, you have earned the right to spend the residual amount of 25,000 rupees for that month. Simple. Isn't it?

Of course, I feel that, it is very simple, but hard to follow. Why? There are some foreigners who were moved by the pathetic situation of the poor, felt like donating all their life savings to the poor, and still felt ridiculed, as if they are trying to save the titanic ship by applying a band-aid to it. May be.. also because... I started hating people(more on it later, in my next blog) and got convinced that people don't deserve my time, money and attention.

Anyways... once you have figured out how much you should be spending (ranging from 0% to 50%) for the society, whatever is left of your income is yours. And now, you have the next big question.... to save? or to spend? Or ... perhaps... how much should I save? and how much should I spend??

Luckily... a wise man named Bhishma taught the younger generations regarding wealth management, few millennia back itself. According to him, a person should feel satisfied if he possess enough wealth to maintain his near and dear for 3 years with that wealth. So, if we translate (misunderstand) that statement to the modern lifestyle, we can (mis)interpret that as... we can retire from our job, if we have saved three times our annual income. Sounds simple. Isn't it? But there is a problem here. The target amount is not 3 times of the present year's annual income, but 3 times of the future year's annual income. Let's say, if you plan to retire after 20 years from now, then, whatever would be your annual income, multiply that with three, and set that as your target amount.

For example... if your annual income right now is 15 lakhs, and your hyper aggressive super optimisitic estimations (A.K.A. greediness, also called day dreams) tell you that your income would be increasing by a factor of 10% every year, you can expect that, after 20 years, you would be earning close to 1 Crore rupees per year.

If you are interested to know how did I get that figures, consider this...

If your income is 15 LPA right now (in 2014), and if you expect a 10% hike, your income would be...

income_in_2015 = income_in_2014 x (1 + 10/100)
= (income_in_2014) x (1.1)
= 15 x 1.1 LPA

And now, for the 2nd year from now (in 2016), if you are again expecting a 10% hike, your income would be 110% of your 2015 income.
income_in_2016 = income_in_2015 x (1 + 10/100)
= (income_in_2015) x (1.1)
= (income_in_2014) x (1.1) x (1.1)
= 15 x (1.1)2 LPA

Similarly, after the nth year from now, your income would be...
income_in_(2014+n) = income_in_2014 x (1.1)n

FORMULA-TIME-1: If you expect an annual hike of h% every year from now, after 'n' years, your income would be...

future_income = current_income x (1 + h/100)n


Which means, after 20 years from now, your annual income would be ...
income_in_2034 = income_in_2014 x (1.1)20
~ 15 x (6.72)
~ 100 LPA

WOW!!! That's a very big amount. But, hey !!! stop thinking about what you would do with that money. We are trying to figre out what is three times the annual income in the future. Remember?

So... if you would like to retire after 20 years from now, you should be saving 3 times your expected future (after 20 years) annual income. Which means that, you should start saving right now, so that you can reach that target of 3 crores ASAP.

That sounds depressing. Doesn't it? 30000000 is a lot of money and u might feel that 1500000 is a very small number in front of it. In fact, 20 times small to be precise. But don't get depressed. I have a good news for you. The savings you do right now are worth much more in the future - thanks to the power of compounding.

FORMULA-TIME-2: If you expect an annual returns of r% on your savings every year from now, then, after 'n' years, your savings worth would be...

future_value = current_value x (1 + r/100)n


Whoa... not so fast. There is a small twist in the story here. If you save your money in a tax saver FD, that promises 9% interest per year, You would be paying upto 30% tax (depending on your tax bracket) on the interest. Which means, you would be getting only 70% of the 9% interest. So, the net return would be... r = 0.7 x 0.09 = 0.063 ~ 0.06 = 6%

For example... if you save 1Lakh this year in an option, that gives you 6% returns, then after 20 years, your savings value would be...
savings_value_in_2034 = savings_value_in_2014 x ( 1.06 )20
~ 1L x 3.2
= 3.2L

But, hey... saving is a habit. Its not a one time commitment. Which means that, you would be saving in 2015, 2016 and so on. For example... if you save another 1L in 2015(1 year from now), then by 2034(20 years from now), the value would be...
savings_value_in_2034 = savings_value_in_2015 x ( 1.06 )19
~ 1L x 3.0
= 3.0L


Which means that if you save 1 lakh now, and 1 more lakh next year, then after 20 years, your total savings value is 3.2 + 3.0 = 6.2 lakhs

So, if you keep saving 1 lakh every year for the next 20 years from now, your total savings would be...
total_savings_by_2034
= 2014_savings x ( 1.06 )20
+ 2015_savings x ( 1.06 )19
+ 2016_savings x ( 1.06 )18
+ ...
+ 2033_savings x ( 1.06 )1
+ 2034_savings x ( 1.06 )0

= 1L x ( 1.06 )20
+ 1L x ( 1.06 )19
+ 1L x ( 1.06 )18
+ ...
+ 1L x ( 1.06 )1
+ 1L x ( 1.06 )0

If you think that the terms here are looking like the terms in a geometric series, then you are 100% right. Indeed they are.

The above expression is of the form....
Sn + 1 = a + ar + ar2 + ar3 + ar4 + ar5 + ... + arn

FORMULA-TIME-3: The sum of the first n terms in a geometric series is...

Sn = a + ar + ar2 + ar3 + ar4 + ar5 + ... + arn-1 = a(1 - rn)/(1 - r)
(I'm tempted to write a blog to understand its derivation. But, relax. I'm not going to scare you now. May be later)


We have to plug-in n = 21 and r = 1.06 and a = 1L in the above formula.
(HOMEWORK: Why not n = 20?)

So, we get total_savings_in_2034
= 1L x (1 - 1.0621) / (1 - 1.06)
~ 1L x (1 - 3.34) / (1 - 1.06)
= 1L x (-2.34) / (-0.06)
= 1L x 39
= 39L

What a shame!!! Its not even 15% of our initial target of 3C.

May be, we can think about saving a little more. How much more? May be just enough to reach the target. And how can we calculate that? By not plugging in any value for 'a' in the formula.

So... we get the algebraic expression...

a x (1 - 1.0621) / (1 - 1.06) ≥ 30000000
=> a x 39 ≥ 30000000
=> a ≥ 30000000 / 39
=> a ≥ 7.7L

If you are a bit tight with those numbers and if you would like to squeeze all the possible optimizations, then, you can use a better r = 1.063, and that gives you a value of a ≥ 7.25L

Which means that, if you keep saving 7.25L every year from now, after 20 years, assuming 6.3% net returns, you would have accumulated 3C!!!

Happy? We have a target. We have a plan. We have our numbers. Are we happy? May be not. Probably 7.25L is a bit too much for us to save per year. That's ok. Fear not earthlings. Mathematics to our rescue. Last time, we have evaluated the expression by using a known 'n' value and an unknown 'a'. What it means is, we have already decided that we should retire in 20 years. And how much should we save every year so that we can retire in peace? was the question.

But, not everyone thinks that way. Some of us might think like...
for example... I can save 5L every year. In how many years can I retire?
In such a case, our expression gets transformed into...

5L x (1 - 1.06n) / (1 - 1.06) ≥ 300L
=> (1 - 1.06n) ≥ 300L x (1 - 1.06) / 5L
=> 1.06n ≥ 3.6 + 1
=> n ≥ log1.064.6
=> n ≥ 26.2 years (MAGIC??? How did I get this number??)

Which means that, if you can save 5L every year from now, you can chose to retire after 25 years as you would have accumulated a wealth of 3C by then.

Now, I'm tempted to write a blog on "understanding exponentials and logarithms"

I wish to write more on mathematics and think a lot more about spending and saving money... but my wife is calling me to join her at the balcony to sip the coffee and enjoy the Bangalore drizzles and relax on our newly bought patio set.

WARNING: Not for the faint hearted
Wise and experienced people say that there is no end to the desires. I have started this blog, explaining the value of a 10 rupee meal for a hungry kid. And ended up doing calculations and setting targets to earn 3 Crores!!! No, I'm not talking about the desire to earn. But, I'm talking about my desire to drag the concepts of fractions, compound interest, geometric series and logarithms into this page. And I somehow feel that there is a lot more to it. But, may be... not for the faint hearted. Just in case, if you happen to be a math-enthusiast, trying to solve some problems, just for the fun of solving them.. here we go.....

So... In the above problems... we assumed that every year, we are saving the exact amount. What if the amount we save is depended on how much we earn? What if the rate of change in our savings (YES!!! You are right. We are heading towards differential equations) is a function of the independent variable named "income" and a dependent variable named "savings_so_far"?

What if the original rule of three times the annual income is not a fail-safe plan? What if the target amount is a function of our life expectancy, our retirement age and a non-linear inflation rate?

What if our decision to spend the money is depended on the mean expected value of our peers' facebook updates and the probability of we reading it? If we have already spent some portion of our earnings, what is the conditional probability that our savings got declined due to the sub-conscious statistical calculations our brain has done after watching our friend spending half his life time savings on a 3 day honeymoon package at a lonely beach? ... and so on.

But, not now. A cup of coffee and an awesome lady are waiting for me.

Blog archive